Esta cápsula es complementaria al artículo Área y Perímetro del círculo.
En el presente apartado, se desarrolla en detalle el cálculo del área de una corona (o anillo) de radios r y (r + dr), donde dr es un diferencial de r, como se aprecia en la siguiente figura:
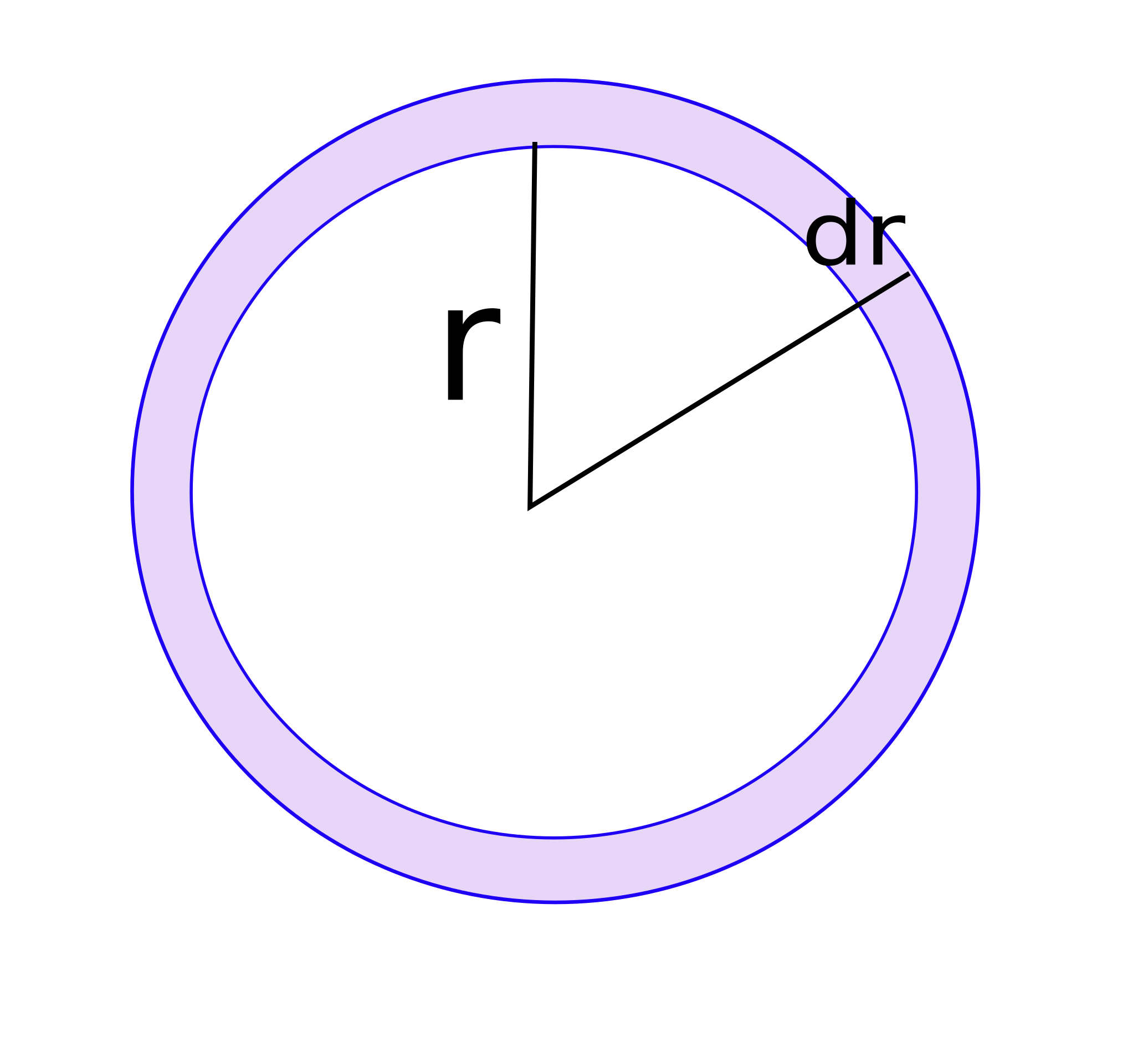
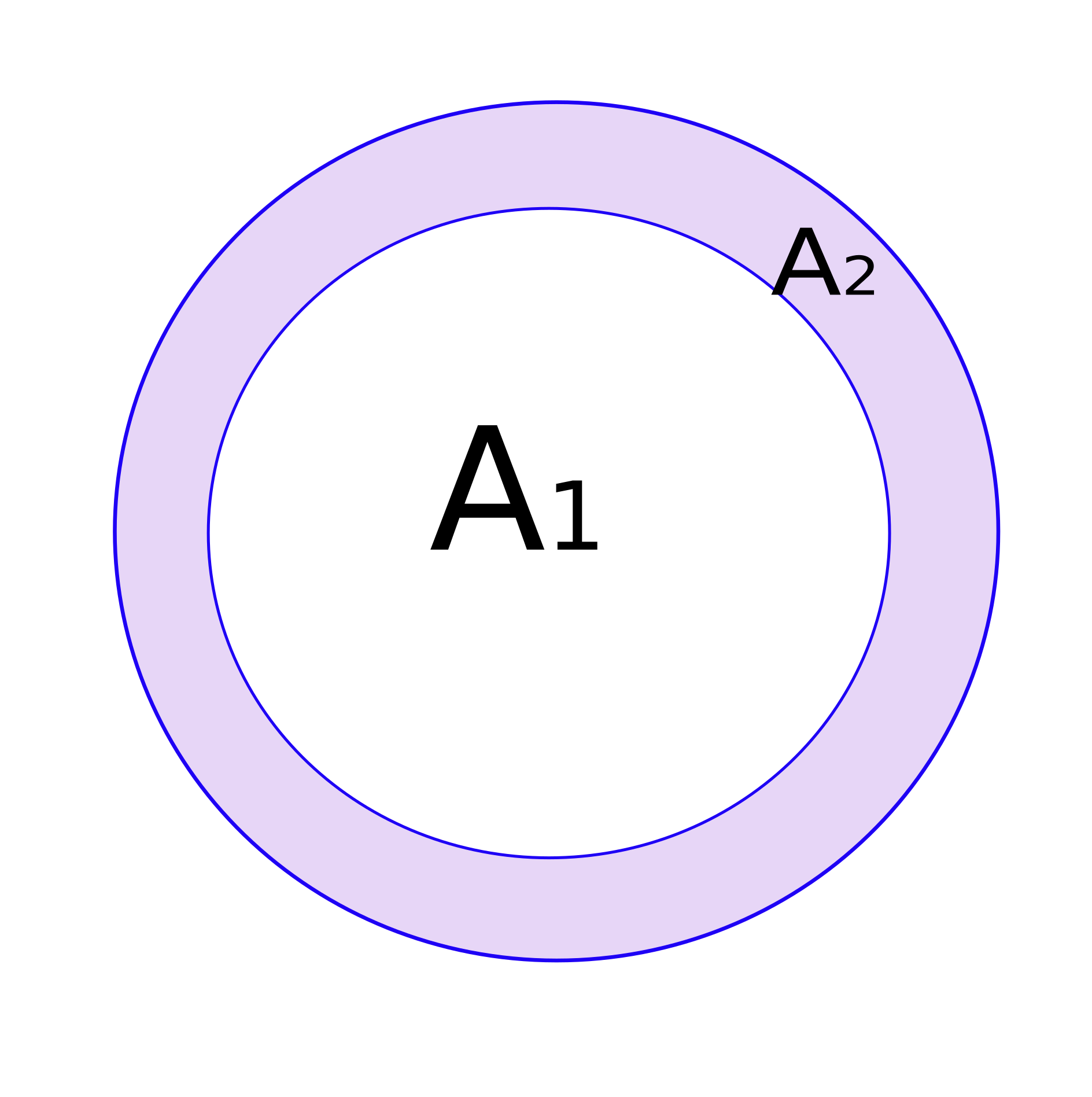
Sea A1 = π.r², el área del círculo de menor tamaño y radio r.
Sea A2 = π.(r + dr)², el área del círculo de mayor tamaño y radio (r + dr)
Entonces, el área de la corona queda determinada por la diferencia Acorona = A2 - A1
Desarrollando el cuadrado del binomio, la expresión del área A2 resulta A2 = π(r²+2r dr+(dr)²)
Dado que dr es un diferencial, es decir, es pequeño con respecto a r, se puede despreciar el último término (dr)². De modo tal, que A2 ≅ π(r²+2r dr) = πr²+2πr dr
Luego, A2 – A1 = (πr²+2πr dr) - π.r² = 2πr dr
Dado que la diferencia de áreas es el área de la corona, llegamos al siguiente resultado:
Acorona = 2πr x dr
Desafiamos a los intrépidos lectores que hayan llegado hasta aquí, a determinar usando papel y lápiz (o lapicera) el volumen de una corona esférica, es decir la figura geométrica análoga para el caso tridimensional.






