El círculo ha sido considerado desde la antigüedad uno de los símbolos de la perfección y de la infinitud. En palabras de Aristóteles:
"Aún más, esta noción circular es necesariamente primaria. Pues lo perfecto es naturalmente anterior a lo imperfecto, y el círculo es algo perfecto. Esto no puede ser dicho de la línea recta." Aristóteles, De Caelo, Capítulo IV
Por definición, un círculo es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio.
Es cosa cierta que el número π entra tanto en la fórmula para calcular el perímetro del círculo P=2πr como el área de dicha figura geométrica A=πr²; sin embargo, no es nada obvio por qué en los dos casos entra el mismo número. Veamos estos dos casos:
1. Si P=2πr, entonces A=πr²
Supongamos que tenemos una torta "perfectamente" redonda y la podamos cortar en unos cuantos trozos triangulares y los vamos acomodando de manera que un triángulo tenga el vértice hacia arriba, el de al lado hacia abajo, y así... Nos queda un rectángulo de ancho igual al radio r y de largo casi igual a la semicircunferencia πr. Como, para un rectángulo, Arect = ancho x longitud; será Arect ≈ r x πr = πr². Lógicamente, si el ángulo con que cortamos la torta es relativamente grande; habrá un cierto error, si vamos decreciendo el ángulo, el error tiende a cero. [1]

2. Si A=πr², entonces P=2πr
Tomamos ahora el camino inverso al anterior. Supongamos que nuestra circunferencia tiene un cierto ancho; después de todo, la dibujamos con un lápiz que tiene, efectivamente, un cierto ancho. Si aceptamos que A=πr²; construimos una corona de radios r y r + dr; por lo que el área de la corona será:
Acorona = 2πr x dr + π x dr² ≡ 2πr x dr + π x dr x dr
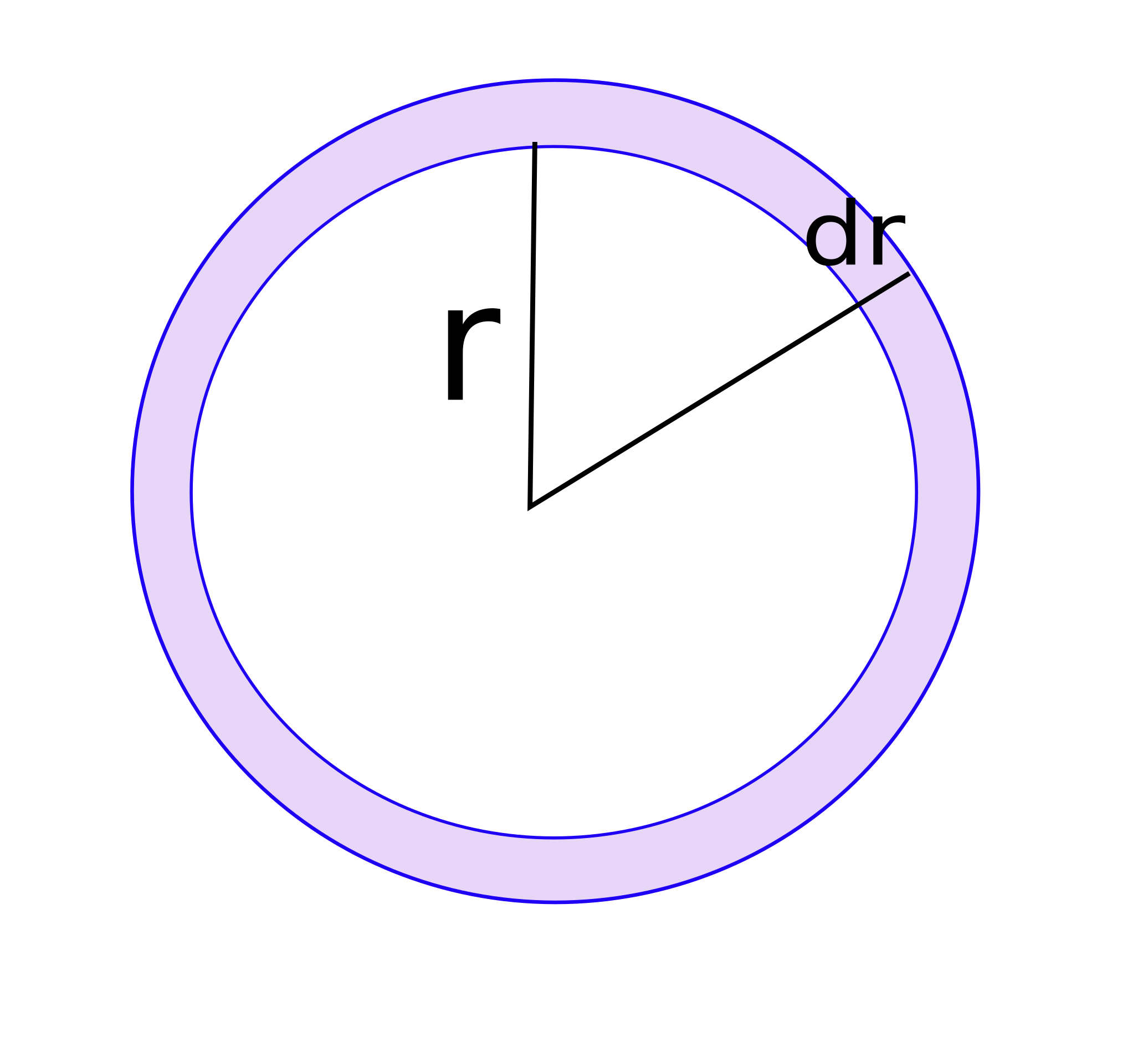
Como podemos tomar el caso en que dr << r (aunque la mina del compás tenga un ancho, será mucho menor que el radio, ¿no?), podemos decir que el segundo término será despreciable respecto del primero y entonces:
Acorona = 2πr x dr
Si decimos que el área de la corona será igual al largo por el ancho, y ancho = dr; entonces nos queda que P=2πr. [2]
3. Algo más con el número π
Si en lugar de tomar un círculo, encerrado por su circunferencia, tomamos una esfera, se podrá probar si es cierto que, dado su volumen V=4πr³/3, entonces la superficie que lo encierra es S=4πr² y viceversa. Estos ejemplos nos dicen que: la derivada del área del círculo es la longitud de la circunferencia y que la derivada del volumen de la esfera es su superficie. ¿Se atreve el lector a demostrar estas aseveraciones?






